谐响应分析

第一节：谐响应分析的定义和目的
第二节：关于谐响应分析的基本术语和概念
第三节：谐响应分析在ANSYS中的应用
第四节：谐响应分析的实例练习

第一节：定义和目的

什么是谐响应分析？
谐响应分析是用于确定线性结构在受正弦荷载作用时的稳态响应,目的是计算出结构在几种频率下的响应,并得到响应随频率变化的曲线.谐响应分析能预测结构的持续动力特性,从而验证设计能否成功地克服共振、疲劳,以及其他受迫振动引起的不良影响.
输入：
已知大小和频率的谐波载荷（力、压力和强迫位移）；
同一频率的多种载荷，可以是同相或不同相的。
输出：
每一个自由度上的谐位移，通常和施加的载荷不同相；
其它多种导出量，例如应力和应变等。

谐响应分析用于设计：
旋转设备（如压缩机、发动机、泵、涡轮机械等）的支座、固定装置和部件；
受涡流（流体的漩涡运动）影响的结构，例如涡轮叶片、飞机机翼、桥和塔等。

为什么要作谐响应分析？
确保一个给定的结构能经受住不同频率的各种正弦载荷（例如：以不同速度运行的发动机）；
探测共振响应，并在必要时避免其发生（例如：借助于阻尼器来避免共振）。

第二节：术语和概念

包含的主题：
运动方程
谐波载荷的本性
复位移
求解方法

运动方程

Fmax =  载荷幅值
I       =  -1
     =  载荷函数的相位角
F1      =  实部, Fmaxcosy
F2      =  虚部, Fmaxsiny
umax=  位移幅值
f  =  载荷函数的相位角
u1  =   实部, umaxcosf
u2  =   虚部, umaxsinf

谐波载荷的本性

在已知频率下正弦变化；
相角y允许不同相的多个载荷同时作用， y缺省值为零；
施加的全部载荷都假设是简谐的，包括温度和重力。

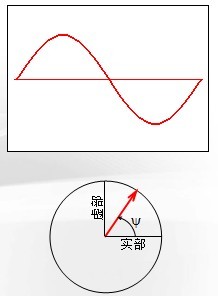
复位移

在下列情况下计算出的位移将是复数
具有阻尼
施加载荷是复数载荷（例如：虚部为非零的载荷）
复位移滞后一个相位角（相对于某一个基准而言）
可以用实部和虚部或振幅和相角的形式来查看
求解方法

求解简谐运动方程的三种方法：
完整法
为缺省方法，是最容易的方法；
使用完整的结构矩阵，且允许非对称矩阵（例如：声学矩阵）。
缩减法*
使用缩减矩阵，比完整法更快；
需要选择主自由度，据主自由度得到近似的 [M]矩阵和[C]矩阵。
模态叠加法**
从前面的模态分析中得到各模态；再求乘以系数的各模态之和；
所有求解方法中最快的。

未完，请看Ansys谐响应分析的概念和步骤（二）

相关标签搜索：Ansys有限元分析  机械设计分析培训  结构静力分析  广州有限元培训  solidworks培训  CAD培训  ansys培训  solidworks  proe培训  运动仿真  有限元FEA  

编辑